Research
Flat Bands
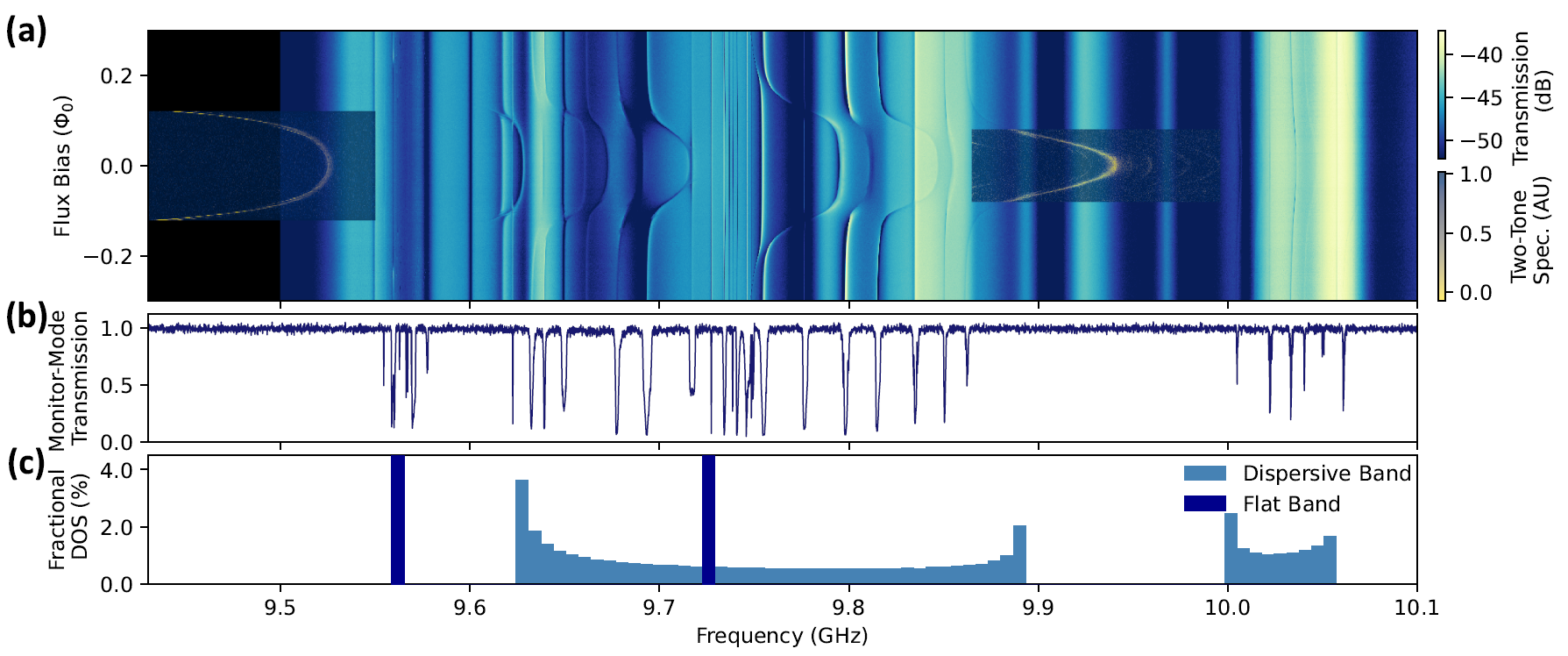
The one-dimensional nature of CPW lattice sites and their inherent deformability leads naturally to the implementation of line graphs with degenerate flat bands. Qubits coupled to these systems will mediate photon-photon interactions within the flat bands. They will also experience novel electromagnetic environments depending on their detuning with respect to the band structure. The resulting photonic bound states have new and controllable forms which give rise to new types of effective spin-spin interactions, including frustrated short-range antiferromagentism in the flat bands.
K. O’Brien, M. Amouzegar, W. C. Lee , M. Ritter, and A. J. Kollár, "Circuit-QED lattice system with flexible connectivity and gapped flat bands for photon-mediated spin models," PRX Quantum 7, 010321 (2026).
A. J. Kollár, M. Fitzpatrick, P. Sarnak, A. A. Houck, "Line-graph lattices: Euclidean and non-Euclidean flat bands and implementations in circuit QED," Commun. Math. Phys. 376, 1909 (2020).
N. M. Sundaresan, R. Lundgren, G. Zhu, A. V. Gorshkov, and A. A. Houck, "Interacting qubit-photon bound states with superconducting circuits," Phys. Rev. X 9, 011021 (2019).
J. S. Douglas, H. Habibian, C.-L. Hung, A. V. Gorshkov, H. J. Kimble, and D. E. Chang, "Quantum many-body models with cold atoms coupled to photonic crystals," Nat. Phys. 9, 326 (2012).
Hyperbolic Lattices

Curvature is fundamental aspect of general relativity, but negatively curved 2D hyperbolic manifolds cannot be isometrically imbedded in 3D Euclidean space. The natural deformability of CPW resonators allows for the implementation of table-top hyperbolic lattices with high curvature. Incorporating qubits into these devices, we can start to examine quantum mechanics in this unique environment.
A. J. Kollár, M. Fitzpatrick, P. Sarnak, A. A. Houck, "Line-graph lattices: Euclidean and non-Euclidean flat bands and implementations in circuit QED," Commun. Math. Phys. 376, 1909 (2020).
A. J. Kollár, M. Fitzpatrick, A. A. Houck, "Hyperbolic lattices in circuit quantum electrodynamics," Nature 571, 45 (2019).
A. A. Houck, H. E. Türeci, and J. Koch, "On-chip quantum simulation with superconducting circuits," Nat. Phys. 8, 292 (2012).
Topological Floquet Systems
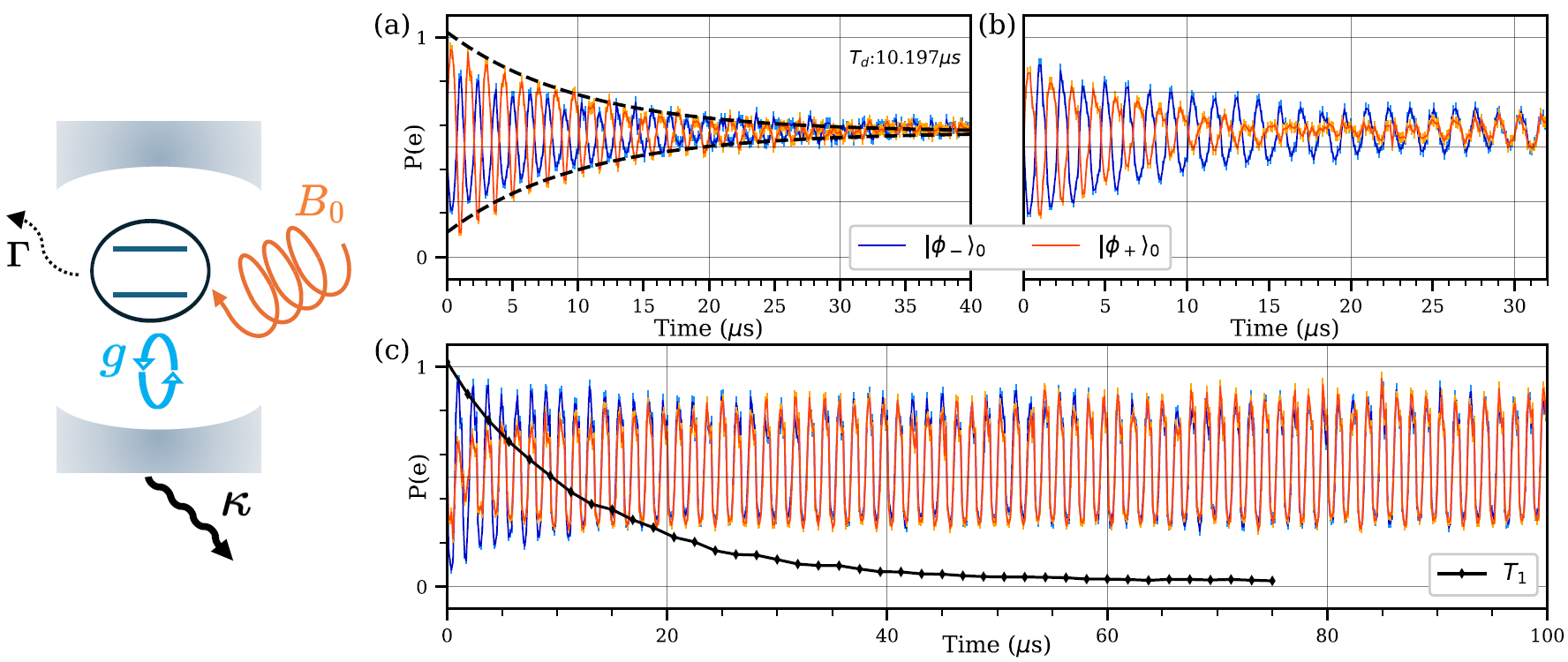
Floquet engineering, in which the properties of the system are qualitatively modified by strong periodic driving, has become an essential part of the quantum mechanic’s toolkit. It enables dynamical control over effective system parameters and the ability to introduce new Hamiltonian terms without changing hardware. In certain regimes, these systems exhibit analogs of the quantum Hall effect in a synthetic space, and as a result, they exhibit non-reciprocal energy transport which is protected by topological invariants of the system and therefore robust to minor variations in the control parameters. Circuit QED provides a unique opportunity for exploring topological Floquet systems due to the combination of long qubit coherence times, strong-light matter coupling, and tunable frequency-dependent dissipation which are native to the hardware platform. Together these ingredients make it possible to realize topological energy pumps in the quantum limit. These devices are potential routes to achieving on-chip non-reciprocal devices which are insensitive to device and drive parameters. Alternatively, the dissipation control provided by microwave cavities can be used to mitigate drive-induced heating, which is otherwise ubiquitous in Floquet systems.
M. Ritter, D. M. Long, Q. Yue, M. Amouzegar, A. Chandran, and A. J. Kollár, “A strong-driving toolkit for topological Floquet energy pumps with superconducting circuits,” Phys. Rev. A 112, 042605 (2025).
M. Ritter, D. M. Long, Q. Yue, A. Chandran, and A. J. Kollár, “Autonomous stabilization of Floquet states using static dissipation,” Phys. Rev. X 15, 031028 (2025).
D. M. Long, P. J. D. Crowley, A. J. Kollár, and A. Chandran, “Boosting the quantum state of a cavity with Floquet driving,” Phys. Rev. Lett. 128, 183602 (2022).
I. Martin, G. Refael, and B. Halperin, “Topological frequency conversion in strongly driven quantum systems,” Phys. Rev. X 7,041008 (2017).
Superconducting Circuits with Spatiotemporal Modulation

All superconducting-qubit devices rely on nonreciprocal elements such as circulators and isolators to facilitate readout and protect the qubits from back-propagating noise. However, conventional implementations are based on magnetic ferrite materials and therefore incompatible with on-chip integration with superconducting qubits. Instead of relying on the Faraday effect and real magnetic fields, spatiotemporal modulation exploits synthetic magnetic fields generated by the spatial propagation and phase-staggered ac modulation to break time-reversal symmetry. Beyond enabling compact on-chip isolators and gyrators, this approach provides a powerful method for engineering direction-dependent couplings in superconducting circuits, giving access to non-Hermitian physics such as exceptional points and robust π-phase (gyration) coupling between degenerate modes. These engineered nonreciprocal interactions open new avenues for both quantum-microwave signal routing and the exploration of synthetic quantum materials in superconducting circuits.
Z. Tu, V. Workman, G. Bahl, A. J. Kollár, “Realization of pure gyration coupling in an on-chip superconducting microwave device,” Phys. Rev. Res. 8, 013049 (2026).
O. E. Örsel, J. Noh, P. Zhu, J. Yim, T. L. Hughes, R. Thomale, and G. Bahl, “Giant nonreciprocity and gyration through modulation-induced Hatano-Nelson coupling in integrated photonics,” Phys. Rev. Lett. 134, 153801 (2025).
Y. Zhuang, C. Gaikwad, D. Kowsari, K. Murch, and A. Nagulu, “Superconducting isolators based on time-modulated coupled-resonator systems,” Phys. Rev. Appl. 21, 054061 (2024).
C. W. Peterson, W. A. Benalcazar, M. Lin, T. L. Hughes, and G. Bahl, “Strong nonreciprocity in modulated resonator chains through synthetic electric and magnetic fields,” Phys. Rev. Lett. 123, 063901 (2019).
B. J. Chapman, E. I. Rosenthal, J. Kerckhoff, B. A. Moores, L. R. Vale, J. A. B. Mates, G. C. Hilton, K. Lalumi`ere, A. Blais, and K. W. Lehnert, “Widely tunable on-chip microwave circulator for superconducting quantum circuits,” Phys. Rev. X 7, 041043 (2017).
Pound-Drever-Hall Readout of Superconducting Qubits
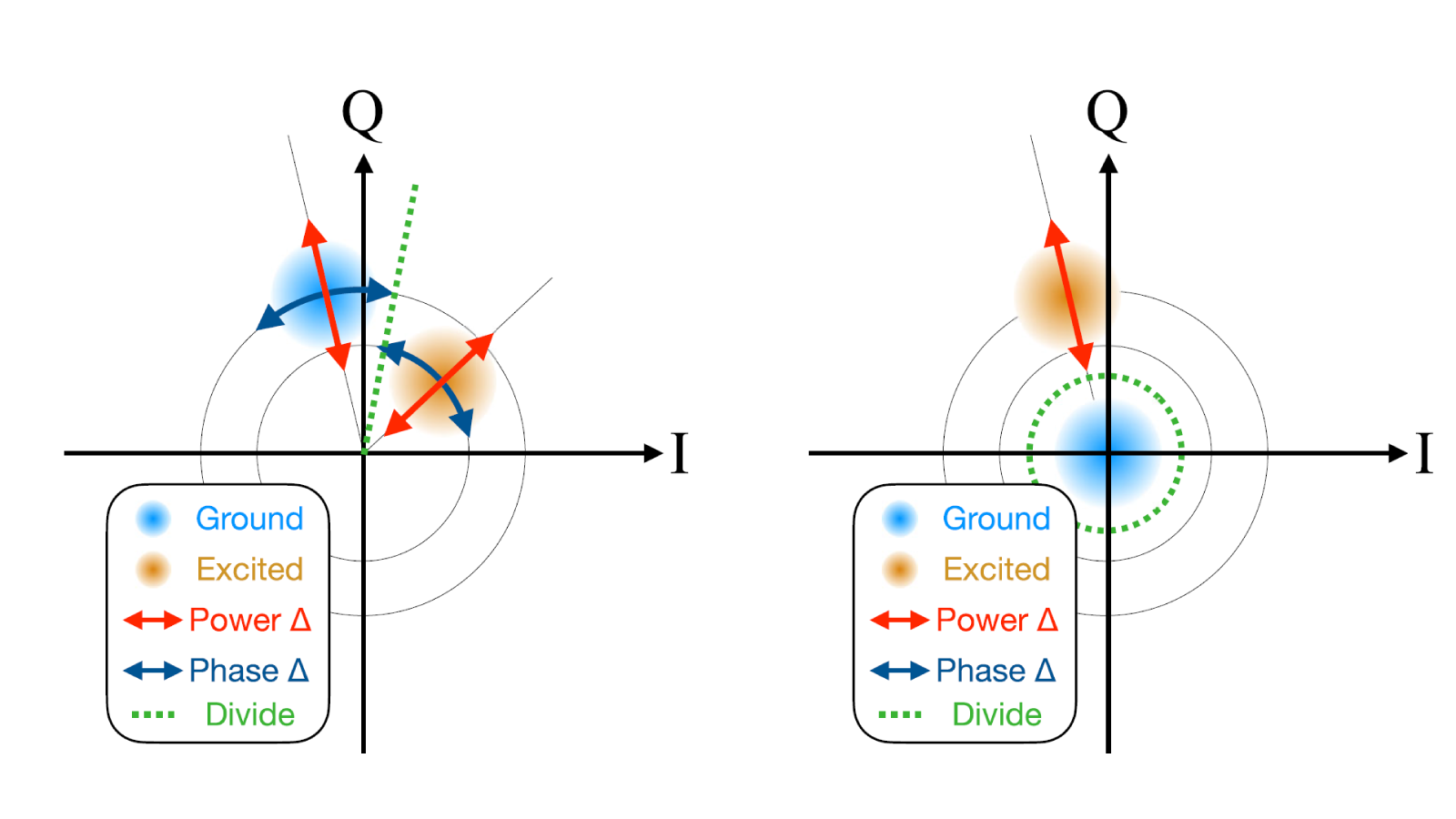
Currently in the circuit QED architecture for superconducting qubits, readout is based on using a homodyne or heterodyne interferometer to sense the frequency of the readout cavity and linear Josephson amplifiers to boost readout signals. The Pound-Drever-Hall (PDH) method, common in the context of optical cavities and lasers, provides an alternative method to sense small changes in a cavity frequency using an off-resonant local oscillator which is co-propagating with the primary probe tone and detected on an E^2 detector. The self-reference and self-heterodyne nature of this method enable precision sensing of the cavity frequency using a non-quantum-limited detector, even if the probe has poor phase (or path length) stability. Microwave PDH has the potential to enable fast, high-stability qubit readout which is insensitive to clocking stability in the microwave measurement electronics.
I. Adisa, W. C. Lee, K. C. Cox, and A. J. Kollár, "The Pound-Drever-Hall method for superconducting-qubit readout," arXiv:2512.03138 (2025).
R.W. Drever, J.L. Hall, F.V. Kowalski, J. Hough, G.M. Ford, A.J. Munley, and H. Ward, "Laser phase and frequency stabilization using an optical resonator," Appl. Phys. B 31, 97 (1983).
E. D. Black, "An introduction to Pound–Drever–Hall laser frequency stabilization," Am. J. Phys. 69, 79 (2001).
T. Lindström, J. Burnett, M. Oxborrow, and A.Ya. Tzalenchuk, “Pound-locking for characterization of superconducting microresonators,” Rev. Sci. Instrum. 82, 104706 (2011).
Superconducting Qubits - Going Hot
All superconducting-qubit devices are currently limited to operating in a dilution refrigerator at temperatures well below 100 mK. These low operating temperatures are forced by the Al Josephson junctions forming the qubits, as well as the microwave control, readout, and reset protocols currently in use. In this LPS qubit collaboratory project, we tackle the challenges of enabling superconducting qubits to operate at higher temperatures, where scaling is much easier due to lower-cost refrigeration and much larger sample capacities and cooling powers. While collaborators at Stanford, Yale, and LPS develop qubit-compatible higher-Tc Jospehson junctions, our UMD/LPS team is developing thermal-photon resistant qubit transitions and readout/reset protocols.
S. Novikov, J. E. Robinson, Z. K. Keane , B. Suri, F. C. Wellstood, & B. S. Palmer, "Autler-Townes splitting in a three-dimensional transmon superconducting qubit," Phys. Rev. B 88, 060503 (2013).
B. Suri, Z. K. Keane , R. Ruskov, L. S. Bishop, C. Tahan, S. Novikov, J. E. Robinson, F. C. Wellstood, & B. S. Palmer, "Observation of Autler–Townes effect in a dispersively dressed Jaynes–Cummings system," New J. Phys. 15, 125007 (2013).
S. J. Srinivasan, A. J. Hoffman, J. M. Gambetta, & A. A. Houck, "Tunable coupling in circuit quantum electrodynamics using a superconducting charge qubit with a V-shaped energy level diagram," Phys. Rev. Lett. 106, 083601 (2011).